Apprenez À Rencontrer L’aire De La Région Englobée Par Des Courbes Complexes Grâce À Des Équations Paramétriques. Explorez Les Techniques Essentielles Pour Résoudre Ce Défi Mathématique.
**équations Paramétriques : Définir Les Courbes Complexes**
- Comprendre Les Fondements Des Équations Paramétriques
- Explorer Les Applications Dans Le Monde Réel
- Décrypter La Représentation Graphique Des Courbes
- Comparaison Avec Les Équations Cartésiennes Classiques
- Étudier Des Exemples De Courbes Célèbres
- Techniques Pour Résoudre Des Problèmes Complexes
Comprendre Les Fondements Des Équations Paramétriques
Les équations paramétriques sont fondamentales pour comprendre la géométrie des courbes complexes. Contrairement aux équations cartésiennes classiques qui relient directement deux variables, les équations paramétriques utilisent une variable supplémentaire, souvent notée “t”, pour exprimer à la fois les coordonnées x et y. Cette approche permet de modéliser des mouvements et des formes de manière plus flexible. Par exemple, une courbe simple, telle qu’un cercle, peut être aisément représentée en utilisant des sinus et cosinus qui, en termes de mouvements, évoquent l’usage de “Count and Pour” dans le cadre d’une pharmacie, où chaque étape est essentielle pour obtenir un résultat précis.
En appliquant cette méthode, il est possible de décrire des figures géométriques très complexes, comme les spirales ou les courbes en boucle. Ces courbes, souvent nommées «élixirs» de la géométrie entre les mathématiques et la physique, acquièrent une nouvelle dimension. En effet, les équations paramétriques offrent une prescription exacte des mouvements dans l’espace. Cela rappelle le travail d’un pharmacien le jour d’un “Pharmageddon”, où chaque détail est primordial pour le bon déroulement des opérations. L’utilisation des équations paramétriques permet ainsi d’optimiser le suivi et la compréhension des dispositifs géométriques dans le monde contemporain.
Pour bien saisir les bases des équations paramétriques, il est impératif de comprendre comment elles diffèrent des autres méthodes. En se concentrant sur le paramètre “t”, nous pouvons traiter la courbe comme un ensemble de points, chacun étant défini dans le temps, similaire à l’approche méthodique d’un “Pharm Tech” lors de la préparation d’un médicament. Avec les bonnes techniques, une analyse minutieuse permet d’évaluer la complexité d’une courbe et de la visualiser clairement, tout en évitant la confusion courante que provoque la comparaison avec les systèmes d’équations cartésiennes. Cette flexibilité en mathématiques est non seulement un accomplissement théorique, mais elle ouvre également des portes vers une multitude d’applications pratiques.
| Élément |
Description |
| Variable |
Utilisée pour exprimer des coordonnées. |
| Paramètre |
Variable supplémentaire “t” permettant d’exprimer une courbe. |
| Flexibilité |
Capacité à modéliser des figures complexes. |
Explorer Les Applications Dans Le Monde Réel
Les équations paramétriques trouvent leur place dans de nombreux domaines de la vie quotidienne, où leur capacité à modéliser des courbes complexes se révèle extrêmement utile. Dans le cadre de la médecine, par exemple, elles permettent de créer des modèles pour la distribution de certains médicaments dans le corps. En comprenant comment un médicament se déplace, les chercheurs peuvent optimiser les doses, ce qui est particulièrement important pour les traitements nécessitant des “scripts” précis et fiables. Cela permet également de réduire le risque d’effets secondaires indésirables qui peuvent survenir lors de l’administration de “narcs” puissants.
Dans le secteur du design et de l’ingénierie, les équations paramétriques permettent de créer des formes et des structures innovantes. Pensez aux voitures et aux avions, dont les courbes aérodynamiques sont souvent réalisées grâce à des représentations paramétriques. Ces modélisations offrent une flexibilité qui améliore non seulement l’esthétique, mais aussi l’efficacité. Les artistes également, notamment dans l’art numérique, utilisent ces techniques pour créer des œuvres captivantes qui intriguent tout en permettant d’encontre a area da regiao englobada pelas curvas.
En architecture, les architectes explorent des solutions uniques à travers des courbes, rendant des bâtiments plus fonctionnels et visuellement stimulants. Les logiciels de conception assistée par ordinateur (CAO) exploitent ces équations pour aider les professionnels à simuler et réaliser des concepts complexes, contribuant ainsi à des projets innovants. Même dans les jeux vidéo, ces représentations permettent de créer des environnements immersifs qui engagent les utilisateurs dans un monde virtuel riche.
Enfin, les domaines de l’animation et des effets spéciaux bénéficient aussi des équations paramétriques. Elles permettent aux animateurs de concevoir des mouvements fluides et réalistes, ajoutant ainsi de la profondeur à leurs créations. Ainsi, l’utilisation de courbes complexes dans ces divers champs montre à quel point les équations paramétriques sont essentielles dans de nombreuses applications réelles, rendant notre monde plus dynamique et fascinant.
Décrypter La Représentation Graphique Des Courbes
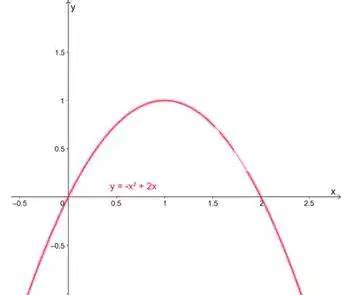
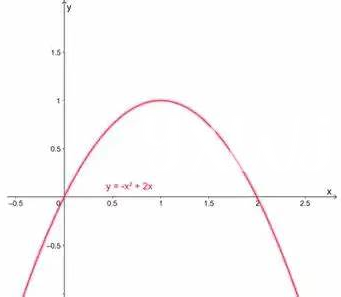
Lorsqu’on aborde la représentation graphique des équations paramétriques, on s’immerge dans un univers fascinant où chaque courbe raconte une histoire. Les équations paramétriques, qui relient des coordonnées (x) et (y) à un paramètre commun, offrent une flexibilité extraordinaire pour modéliser des formes complexes. En visualisant ces courbes, chaque point représente une position spécifique à un instant donné, ce qui permet de suivre leur évolution dans le temps. Cette approche s’avère particulièrement utile dans des domaines comme la physique ou l’ingénierie, où il est crucial de connaître les variations d’une trajectoire.
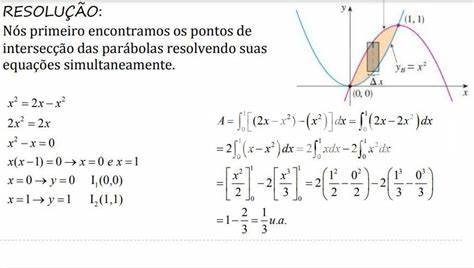
La beauté des courbes paramétriques réside également dans leur capacité à entourer des zones spécifiques. Par exemple, on peut facilement encontre a area da regiao englobada pelas curvas en utilisant des techniques d’intégration pour calculer les surfaces. Cette méthode permet d’obtenir des résultats concrets à partir de l’immatériel, ouvrant la voie à des applications variées, de l’animation visuelle à la modélisation scientifique.
En comparant les courbes paramétriques avec celles des équations cartésiennes, on se rend compte que la première offre une perspective plus dynamique. Les courbes paramétriques peuvent décrire des mouvements circulaires ou sinusoïdaux d’une manière plus intuitive que leurs homologues cartésiennes. En intégrant des notions comme la continuité et la dérivabilité, on élargit notre compréhension des comportements mathématiques, ce qui permet d’apprécier davantage la richesse et la complexité des structures géométriques que nous pouvons créer.
Comparaison Avec Les Équations Cartésiennes Classiques
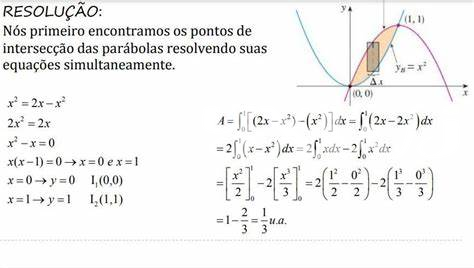
Les équations paramétriques se distinguent nettement des équations cartésiennes classiques. Dans ce dernier cas, une courbe est généralement décrite par une relation directe entre les coordonnées (x) et (y). Cela signifie que pour chaque valeur de (x), il existe une valeur unique de (y). En revanche, avec les équations paramétriques, nous introduisons un troisième élément : un paramètre, souvent noté (t), qui lie les coordonnées (x) et (y) en une structure plus flexible et dynamique. Cette approche permet de générer des courbes complexes et d’explorer des formes que les équations cartésiennes ne peuvent pas facilement décrire.
Les courbes paramétriques offrent par ailleurs une alternative très efficace pour le calcul de l’aire de la région englobée par les courbes. En utilisant les intégrales sur le paramètre (t), il est possible de déterminer des propriétés géométriques avec une précision accrue. Généralement, ce type de calcul n’est pas aussi direct avec les équations cartésiennes, où la séparation des variables peut s’avérer difficile. Ainsi, cette flexibilité dans la représentation permet aussi une plus grande variété dans les applications pratiques, telles que la modélisation de trajectoires en physique ou la conception assistée par ordinateur.
Finalement, il est important de noter que, malgré ces avantages, la transition entre les deux formes de représentation nécessite de bien maîtriser les concepts fondamentaux. Les équations cartésiennes classiques sont souvent plus accessibles pour les novices et fournissent une base solide sur laquelle se construit la compréhension des équations paramétriques. Cependant, pour ceux qui souhaitent approfondir leurs connaissances, la compréhension et l’exploration des équations paramétriques peuvent s’avérer être une voie enrichissante et passionnante.
Étudier Des Exemples De Courbes Célèbres
Les courbes célèbres représentent des exemples fascinants d’équations paramétriques qui ont captivé les mathématiciens depuis des siècles. Prenons par exemple la spirale d’Archimède, qui peut être décrite par les équations ( x(t) = t cdot cos(t) ) et ( y(t) = t cdot sin(t) ). Cette courbe engageante illustre comment une simple variable peut créer une symmetry complexe en s’élargissant infiniment. En considérant la région englobée par cette courbe, on peut explorer des concepts géométriques intéressants qui ont des applications pratiques dans des domaines comme l’architecture et le design.
Un autre exemple marquant est la courbe de Bézier, utilisée notamment dans la conception graphique pour modéliser des trajectoires fluides. Les équations paramétriques qui la définissent permettent de comprendre les mouvements dans l’espace, rendant le travail des artistes et des designers beaucoup plus intuitif. En combinant ces exemples, nous pouvons mieux appréhender les nuances des courbes complexes et comment elles peuvent être appliquées de manière efficace dans des projets concrets, tout en développant une sorte de pharmacopée algorithmique qui pourrait transformer notre approche de l’espace et de la visibilité.
| Courbe |
Équations Paramétriques |
Applications |
| Spirale d’Archimède |
x(t) = t * cos(t), y(t) = t * sin(t) |
Architecture, design |
| Courbe de Bézier |
Utilise des points de contrôle pour définir le chemin |
Graphisme, animation |
Techniques Pour Résoudre Des Problèmes Complexes
Quand il s’agit de résoudre des équations paramétriques, il est essentiel d’adopter une approche systématique et structurée. Pour commencer, décomposer le problème en éléments plus petits peut s’avérer bénéfique. En identifiant les paramètres distincts qui définissent la courbe, un étudiant peut utiliser des substitutions et des simplifications pour mieux gérer des situations complexes. Ce processus rappelle la gestion des prescriptions médicamenteuses : tout comme un pharmacien doit souvent interpréter les “Sig” pour comprendre les instructions de médication, il en va de même pour comprendre les paramètres d’une équation.
Ensuite, maîtriser la visualisation est un atout majeur dans cette démarche. Utiliser des outils graphiques permet de mieux appréhender les comportements et les interactions des courbes. De plus, établir des équivalences avec les équations cartésiennes peut fournir une aide précieuse, tout comme on pourrait faire un “Meds Check” pour s’assurer qu’un patient reçoit le bon traitement. Une fois ces éléments en place, la résolution des problèmes complexes devient une question de pratique et d’expérimentation, en s’entraînant à ajuster les paramètres de manière à atteindre les résultats souhaités, permettant ainsi de s’orienter dans le monde dynamique des équations et de la modélisation.



